What happens if you play billiards on an elliptical table, with no friction?

One way of defining an ellipse is in terms of two points, each of which is called a focus point. The ellipse is then the locus of all points such that the sum of the distances from these two foci is always a constant. You can visualise it like this: put a loop of string around pins located at the foci, then pull the string taut at one point using a pencil. If you then slide the pencil while keeping the string tight, then the shape that you get is an ellipse.

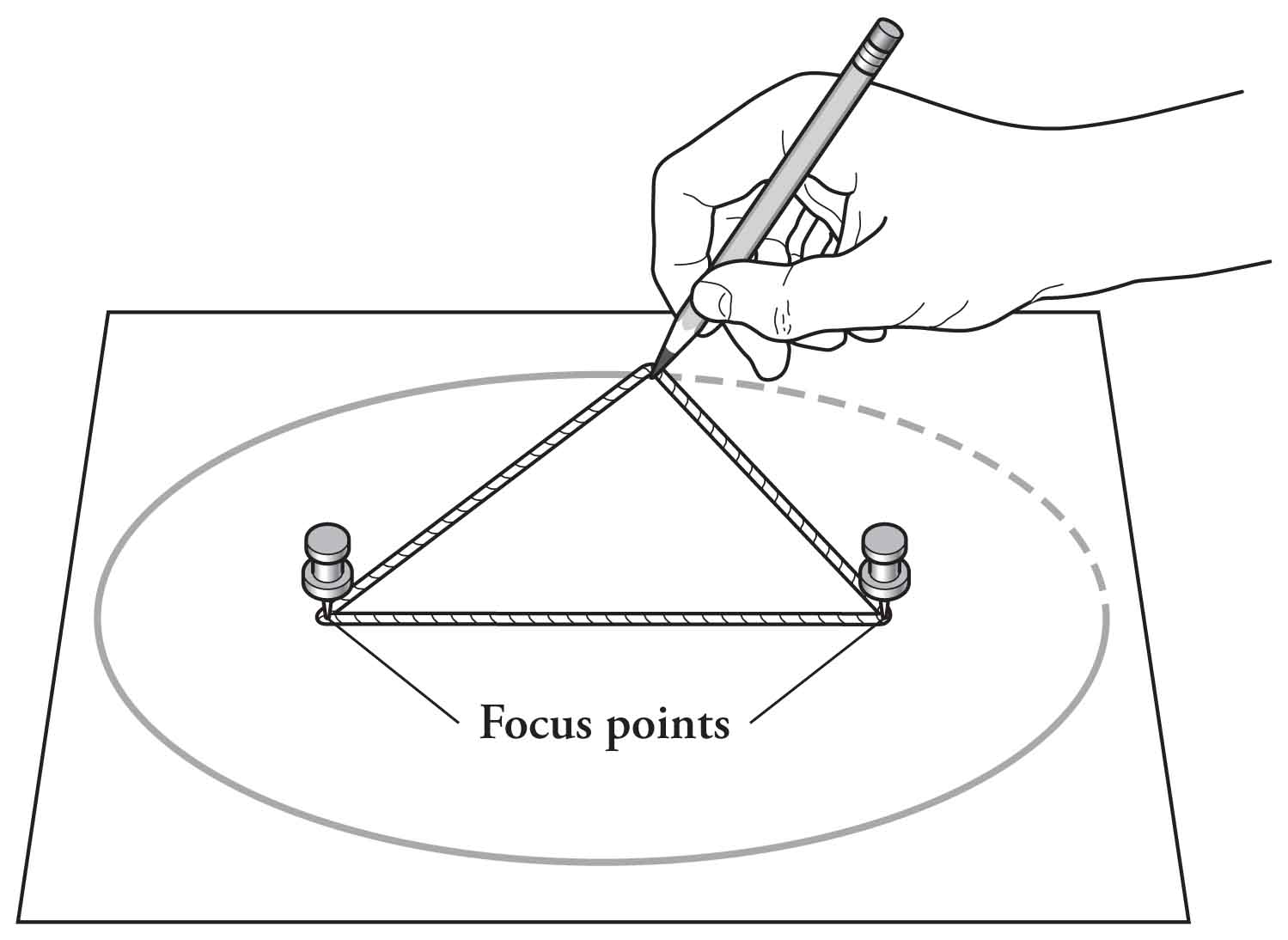
Image source: Alex Through the Looking Glass

The reflective property of ellipses

What’s so cool about this definition? One thing that I think it brings to the table is that it allows us to intuitively understand a curious property of ellipses. Suppose you want to play a game of billiards (or pool, or snooker, or whatever takes your fancy), but instead of playing on a rectangular table, you play it on an elliptical table. What happens if when you hit the billiard ball, it passes through one of the focus points of the elliptical table?

Regardless of the initial direction, after passing through one focus, the billiard ball reflects off the ellipse and passes through the other focus.

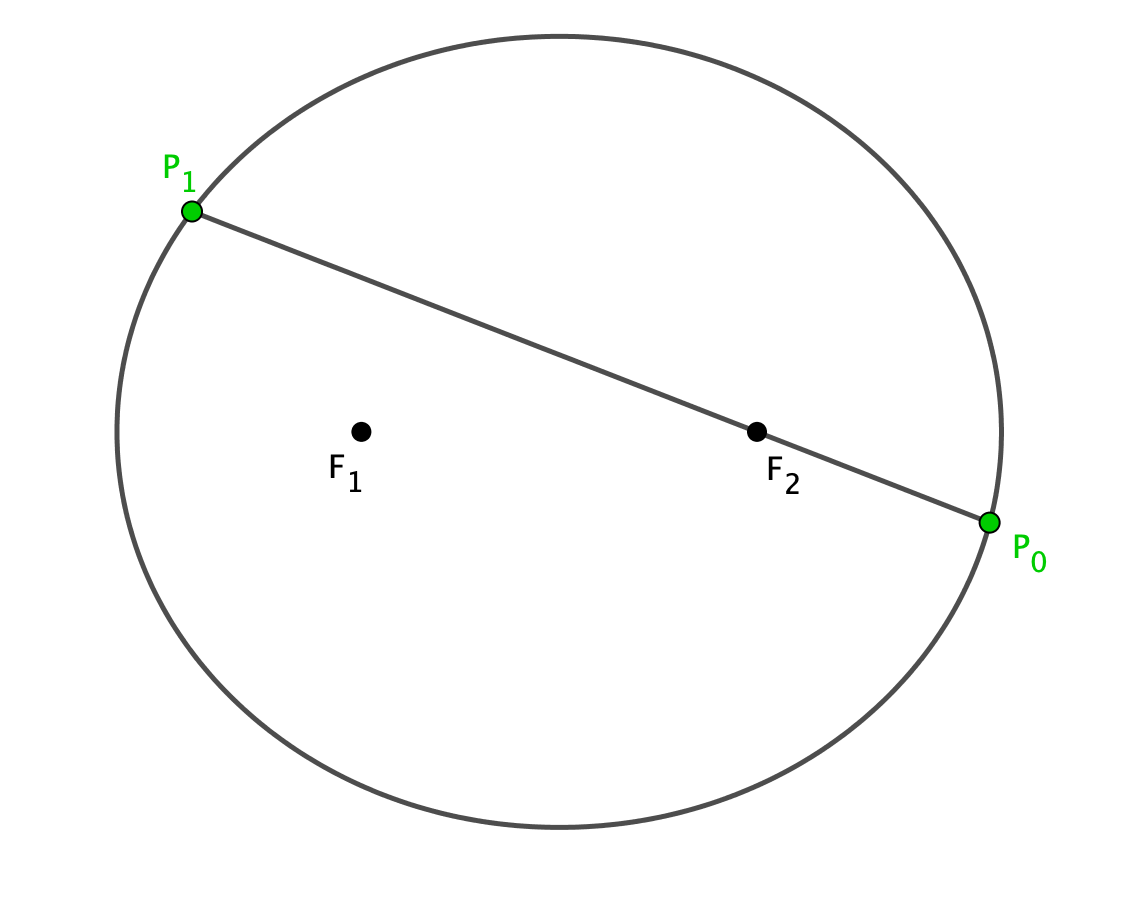
Suppose you hit a billiard ball at \(P_0\), sending it through the focus point \(F_2\) to \(P_1\). What happens next?

But why stop there? What happens after the ball bounces off the elliptical table a second time?

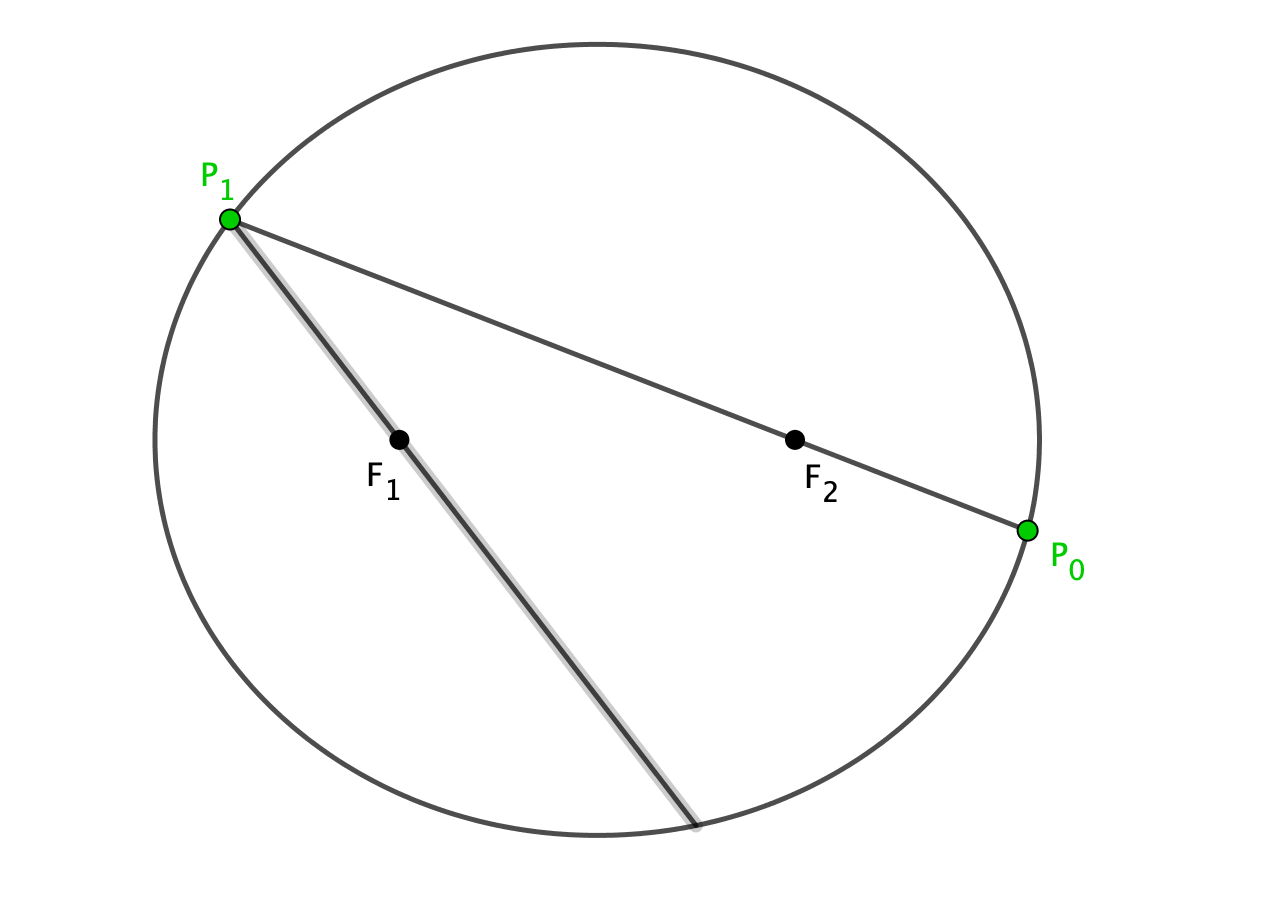
And again…

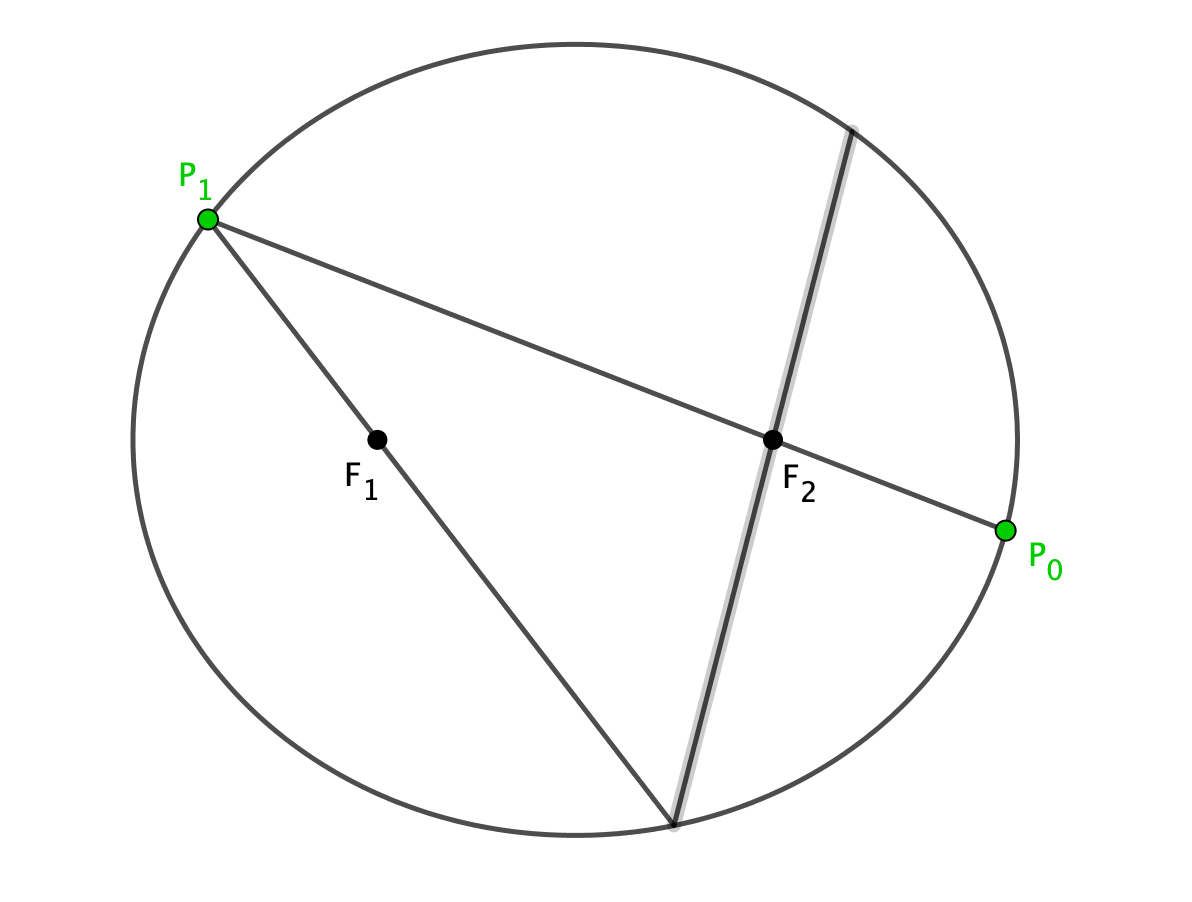
Each time the ball passes through one of the foci, it reflects off the elliptical table and passes through the other focus. Let’s take this further - what happens if we keep doing this?

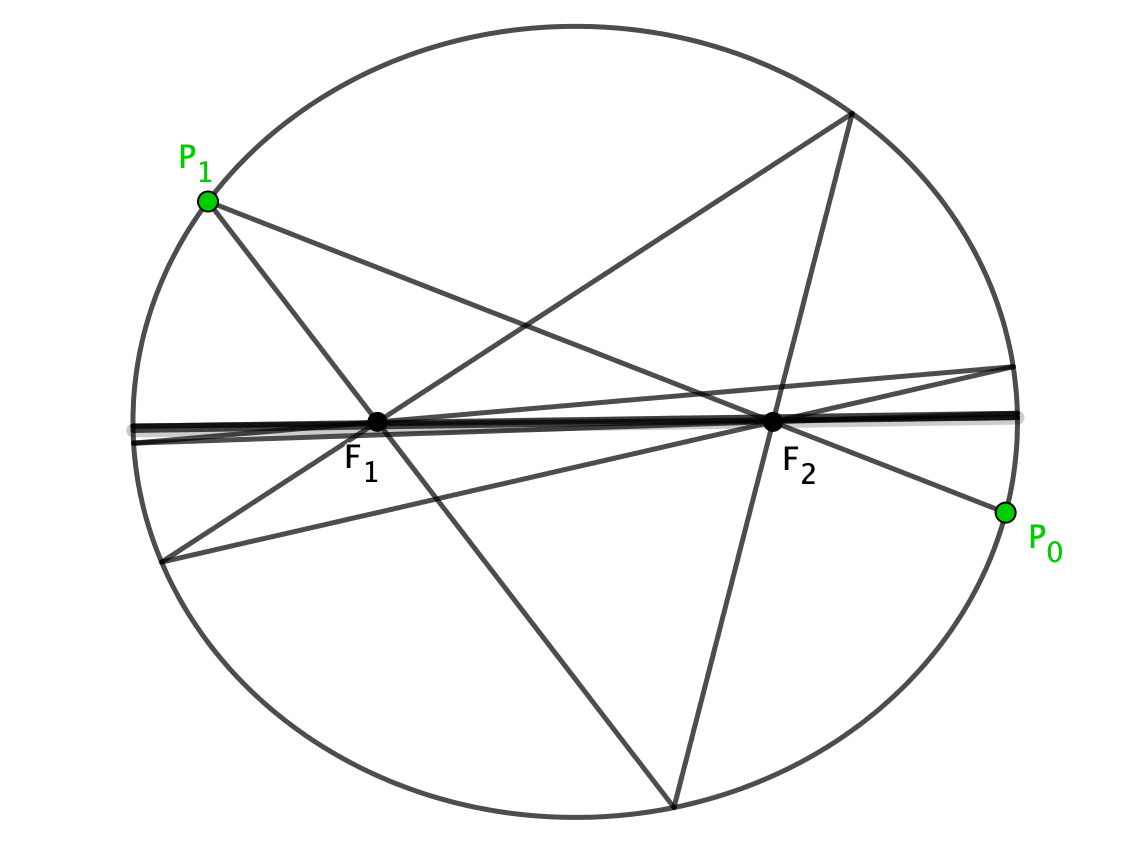
We can see that after many bounces, the trajectory of the ball converges to the horizontal.

This poses the question: why does this happen? There are many ways to attack this problem, some of which are heftier than others (coordinate geometry!). If you’re familiar with Fermat’s principle of least time, then you can directly apply it here but with a billiard ball instead of light rays. In this case, we’re trying to get from the focus \(F_2\) to \(F_1\), and we’re subject to the constraint that the ball must also touch the elliptical table. But we know from the aforementioned definition of the ellipse that any such path must have exactly the same length! So this means that no matter the direction with which the billiard ball passes through \(F_2\), any path that it takes to \(F_1\) is a reflection, and so we get the reflective property of ellipses.

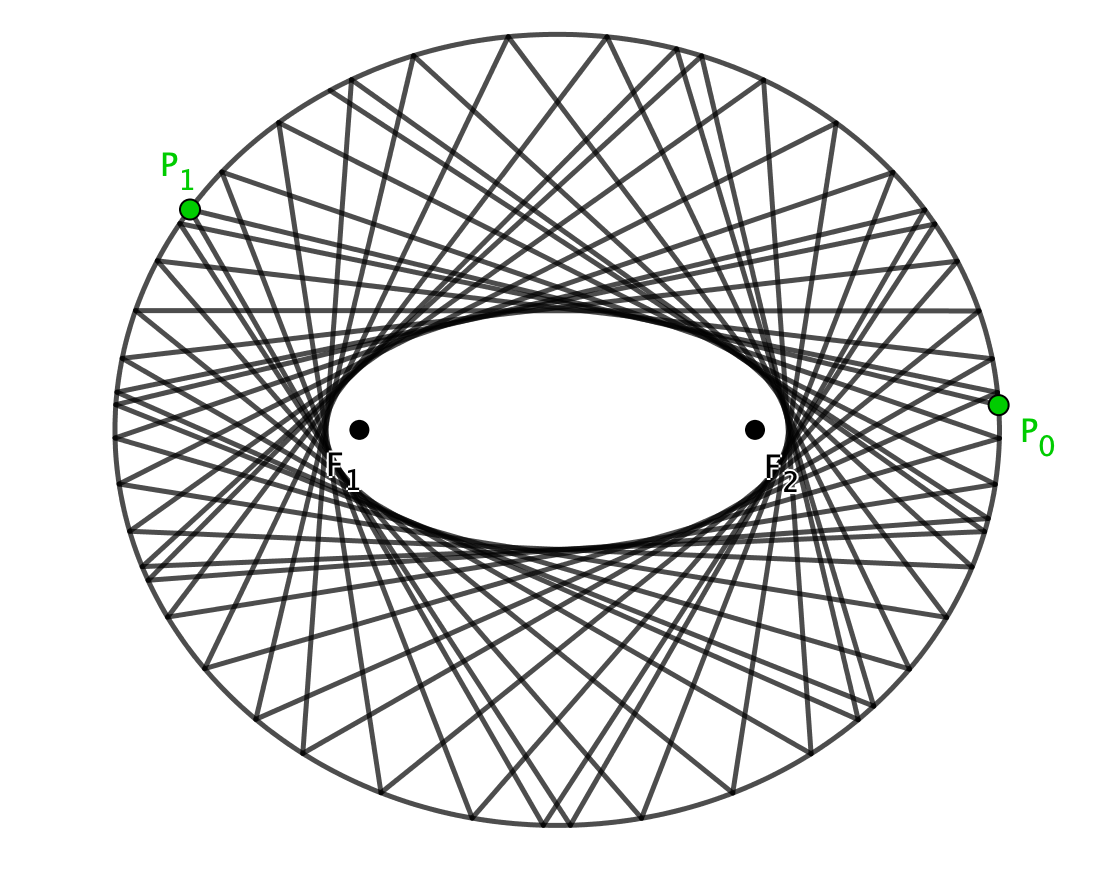
Caustic curves

Interestingly, what we get is an elliptical caustic curve that shares the same foci as the elliptical table, and so these are confocal ellipses.

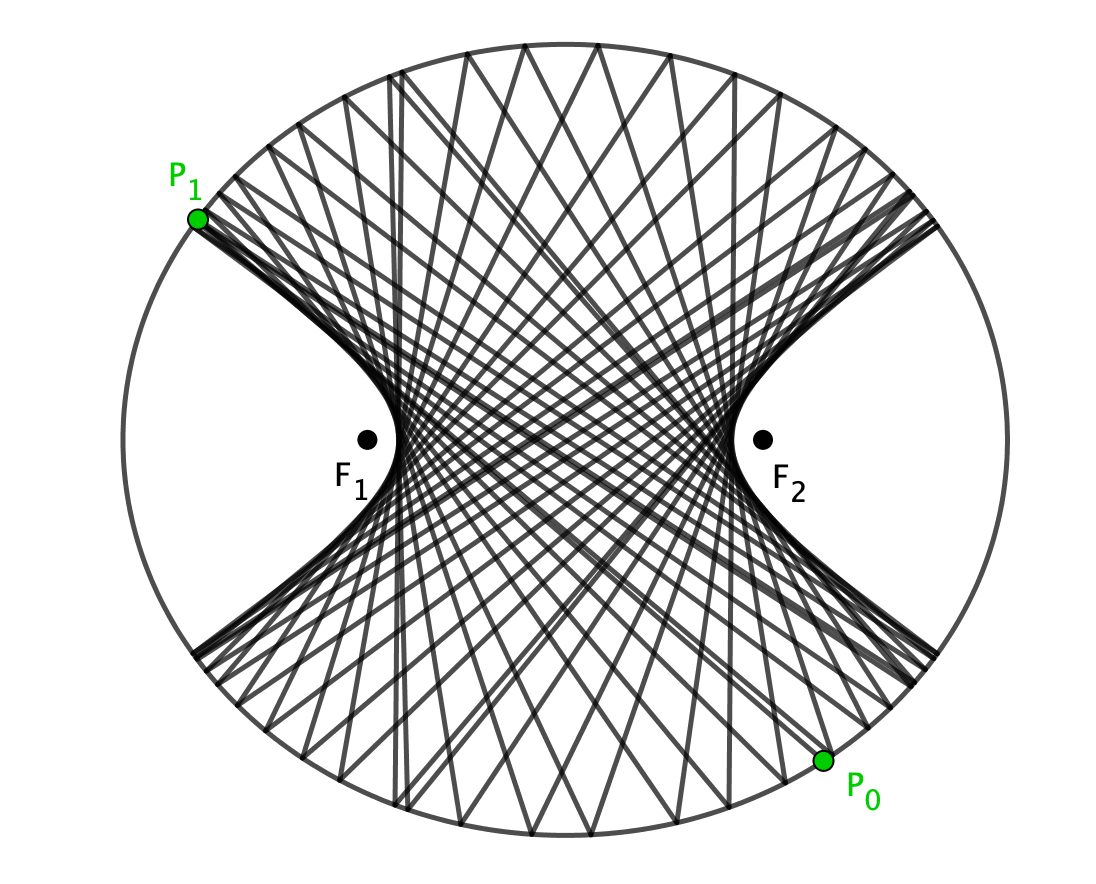
What if we change things slightly and have the ball initially pass between the two foci? In this case we get a confocal hyperbola, which is really interesting.

Another interesting thing to note is that the caustic ellipse can be obtained via a conformal map (locally angle preserving). If the elliptical table has the equation

\begin{equation} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \end{equation} where \(a\) and \(b\) are the semi-major and semi-minor axes respectively. The the conformal caustic has equation

\begin{equation} \frac{x^2}{a^2 + \lambda} + \frac{y^2}{b^2 + \lambda} = 1, \end{equation} where \(\lambda\) is a constant. When the denominator of the first term satisfies \(a^2 + \lambda > 0\), then the caustic is an ellipse. If instead \(-b^2 < \lambda < -a^2\), then it is a confocal hyperbola.

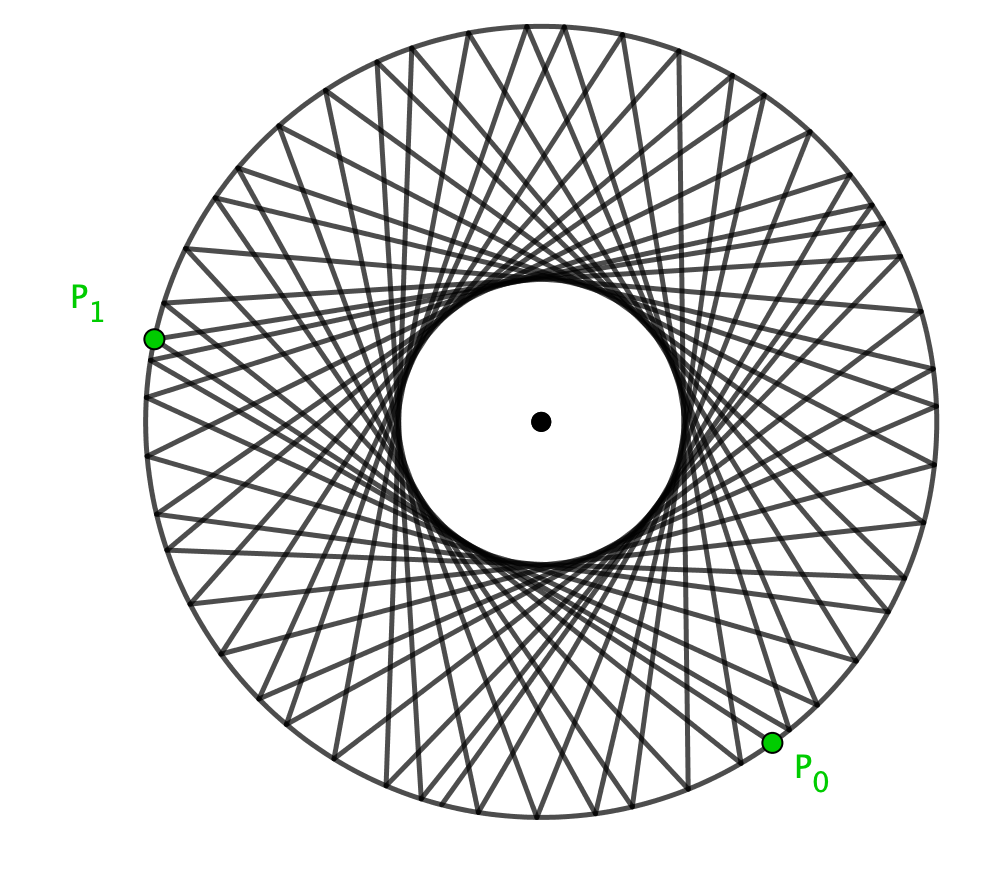
If we play around with the eccentricity of the ellipse (by changing the positions of the foci), then we get the special case of the circle. In this case, we get a concentric circle as a caustic, as you might expect.

Simulation and Resources

I’ve made a GeoGebra applet that shows this for 50 reflections in the ellipse, which you can play around with. You can find more information on my GeoGebra page or in my GitHub repository.

GeoGebra

You can change the eccentricity of the ellipse, and also hide or show the caustic curve (in blue) to see how things change. The initial trajectory of the billiard ball is uniquely determined by the positions of \(P_0\) and \(P_1\).

Resources

There are also other situations that could be investigated, such as the high-symmetry case where the eccentricity becomes zero, and analysing periodic orbits using a group/number theoretic approach. If you’re interested in finding out more, I recommend:

• Elliptical Pool Table (Numberphile video)
• The Birkhoff billiards page at dynamical-systems.org
• Math 188r Dynamical systems lecture notes by Oliver Knill

---